A
review on methods to estimate a CT from MRI data in the context of MRI-alone RT
Type of article: Review
Wafa Boukellouz1 and Abdelouahab Moussaoui
Department of informatics, Faculty of sciences, Ferhat Abbas University,
Setif, Algeria.
Abstract
Background: In recent years,
Radiation Therapy (RT) has undergone many developments and provided progress in
the field of cancer treatment. However, dose optimisation each treatment
session puts the patient at risk of successive X-Ray exposure from Computed
Tomography CT scans since this imaging modality is the reference for dose
planning. Add to this difficulties related to contour propagation. Thus,
approaches are focusing on the use of MRI as the only modality in RT. In this
paper, we review methods for creating pseudo-CT images from MRI data for
MRI-alone RT. Each class of methods is explained and underlying works are
presented in detail with performance results. We discuss the advantages and
limitations of each class.
Methods: We classified recent
works in deriving a pseudo-CT from MR images into four classes:
segmentation-based, intensity-based, atlas-based and hybrid methods and the
classification was based on considering the general technique applied.
Results: Most research focused
on the brain and the pelvic regions. The mean absolute error ranged from 80 to
137 HU and from 36.4 to 74 HU for the brain and pelvis, respectively. In
addition, an interest in the Dixon MR sequence is increasing since it has the
advantage of producing multiple contrast images with a single acquisition.
Conclusion: Radiation therapy is
emerging towards the generalisation of MRI-only RT thanks to the advances in
techniques for generation of pseudo-CT images and the development of
specialised MR sequences favouring bone visualisation. However, a benchmark
needs to be established to set in common performance metrics to assess the
quality of the generated pseudo-CT and judge on the efficiency of a certain
method.
Keywords:MRI-alone RTP, Pseudo-CT, Electron density,
Radiotherapy treatment planning.
Corresponding author: Ms Wafa Boukellouz
Department of informatics, Faculty of sciences, Ferhat Abbas University, Setif,
Algeria. Email:
w_boukellouz@outlook.fr
Received:
September 05, 2017, Accepted: October 30, 2017, English editing: January 14,
2018, Published: March 19, 2018.
Screened
by iThenticate.©2018KNOWLEDGE KINGDOM PUBLISHING.
1. Introduction
Radiation Therapy (RT) is a treatment that
consists of delivering high doses of ionising radiation to a tumourin order to
destroy it. This treatment option has undergone many developments starting from
whole body radiation therapy to conformal radiotherapy; this latter allows to
deliver a limited number of high doses to cancerous cells devised on small
fractions while keeping the dose delivered to the surrounding organs minimal.
One important step in the process of Radiation Treatment Planning (RTP) is
imaging, where a series of imaging studies, usually CT, MRI and PET scans are
performed. Among these, Computed Tomography (CT) is used as the primary imaging
modality, as the dose planning relies on the electron density information from
CT scans (see Figure 1 for an example of 4D dose distribution resulting from a
carbon ion spot beam, computed on a 4D CT volume). However, accurate
delineation of a tumour and other organs on CT scans is difficult because of
its poor soft tissue contrast. In the case of prostate and rectum cancers,
studies have shown that the prostate and rectum volumes are overestimated when
contoured on CT scans compared to the delineated volumes on MR images (1, 2).
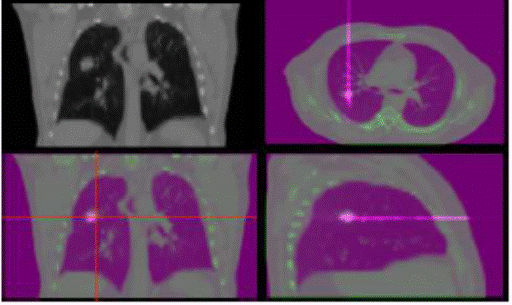
Figure .1 4D dose distribution resulting from a carbon
ion spot beam computed on a 4D CT image.
Hence, Magnetic Resonance Imaging (MRI) is
used jointly with CT for its excellent soft tissue contrasts that are based on
multiple contrast parameters (3). MRI is characterised by its superior soft
tissue contrasts that allow distinguishing several tissues and organs (see
Figure 2). It is based on physical characteristics of Nuclear Magnetic
Resonance (NMR) of water protons in the body. Radio waves are used to excite
the nuclei of hydrogen atoms within the patient's body. These radio waves are
subsequently re-emitted by the patient in a manner, which is characteristic of
the NMR properties of the tissues involved, detected, digitised and processed
by a computer and displayed as tomographic slices revealing the distribution of
different tissues.
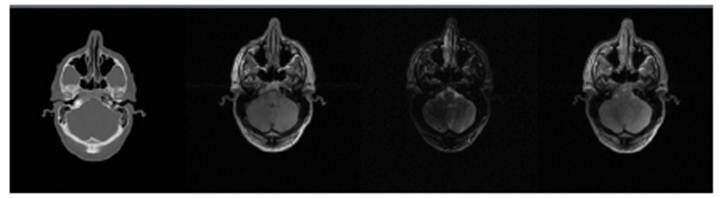
Figure .2 Brain CT, T1-weighted, T2-weighted and
proton density MRI slices (from left to right) showing the different contrasts
provided by MRI compared to CT.
Thus, MRI is used for defining the target
volume and Organs At Risk (OAR). Afterwards, these contours are transferred to
CT data using contour propagation techniques (4-8) for dose calculations;
contour propagation is achieved by spatially aligning the CT and MR images
using image registration techniques (9). However, this task can result in a
mean registration error of approximatively 2 mm in body organs such as the
prostate, which can cause a significant shift in target volume definition,
consequently leading to a reduction in treatment accuracy and efficiency
(10-12).
Nowadays, studies strive for using MRI as the
only modality in radiation therapy to take advantage of its soft tissue high
contrast, remove registration uncertainties, reduce financial cost and imaging
time and limit radiation exposure from X-Ray scans. Moreover, with the
increasing development of MRI, this imaging modality has become the tool of
choice for many treatments. Therefore, the need for a strategy that can combine
the dose planning and an excellent structures visualisation has called for an
MRI-alone RTP; the idea is to derive a CT or a so-called pseudo-CT from MRI
data. Nevertheless, MRI cannot be used directly for dose planning because MR
intensities correlate with proton densities and relaxation properties, whereas
dose calculations require data on Electron Density (ED) derived from CT scans.
Therefore, ED information needs to be assigned to MR images.
The earliest approaches for assigning ED
information to MR images consisted of setting the whole body to a uniform bulk
density value (usually corresponding to water) and assigned a different bulk
density for bone volume (13-16) Beavis et al. (13) used a water method for an
MRI-alone radiation therapy workflow. The whole body was set to a homogeneous
electron density value of water. Despite its simplicity, this approach cannot
generate a reliable CT reference for dose calculation and may lead to erroneous
results (17).
An improved approach that segments the anatomy
into different tissue classes and assigns a uniform bulk density values for
each class (14, 18, 19, 15, 16, 20). In (14), contoured CT images were used to
derive electron density information using two approaches: one consists in
setting the whole body to a homogenous CT value of water (0 HU), and the other
approach created a bone + water image were bone was manually contoured on CT
scans, these contours were assigned an average Hounsfield Unit (HU) value of
four patients (320 HU). The rest of the voxels were assigned the value of 0 HU.
The bone + water approach was applied to segmented MR images and assigned the
corresponding derived HU values to each segment. Chen et al. (18) delineated
the bony structures of the pelvic (femoral heads and scrum) manually on
T2-weighted sequences and assigned to them a bulk value of 2.0 g/cm3in order to
perform an MRI-based Intensity-Modulated Radiation Therapy (IMRT). Dose
differences between the CT-based and their MRI-based dose plans were within the
accepted clinical criteria (2%).
In (19), Eilertsenet al. investigated the
dosimetric accuracy of treatment plans created from pseudo-CT images estimated
using three approaches; the first approach is water-based where the whole
volume was set to the value of 1.02 g/ cm3. The second approach assigned the
value of 1.3 g/ cm3 for the segmented pelvic bone and the rest of the body was
assigned the value of 1.02 g/ cm3. The last approach is similar to the second
one, only differed by assigning the bone a value of 2.1 g/ cm3. Results for
dose distribution differences for IMRT plans revealed that the second approach
(with bone assigned a bulk value of 1.3 g/ cm3) performed better with the
relative difference of the mean dose to the Clinical Target Volume (CTV) equal
to -1.6% ± 0.4, compared to -2.8% ± 0.5 and -4.3% ± 1.7 for the water and the
“2.1 g/ cm3”-bone approaches, respectively. Furthermore, authors mentioned that
the dose inhomogeneity in the CTV increases when bone is set to the value of
2.1 g/ cm3.
Lambert et al. (16) assigned the bulk value of 1.13 g/ cm3
for the pelvic bone in MR images to investigate on the dosimetric accuracy of
the generated plans compared to the full density CT-based (Gold standard) and
water-based plans. Results showed an average dose difference of 1.3% between
the gold standard and the MRI-based bone bulk density plan compared to 2.5% of
dose differences between the MRI-based bone bulk density plan and the water
approach. Hoogcarspel et al. (21)
investigated the dosimetric accuracy of different bulk density approaches
forcreating a pseudo-CT from MRI data in the context of Stereotactic Body
Radiation Therapy (SBRT) for spine metastases. Five different pseudo-CT images
were generated based on different tissue segmentations (water density, lung density,
bone density, fat density and heterogeneous density). The heterogeneous density
pseudo-CT was generated by aligning fat and water Dixon-based MR sequences to a
CT containing contours for the target volume. This was done to assign the
electron density value of the target volume to the MR image. Therefore,
creating a pseudo-CT containing the electron density values of fat, water, lung
and bone. The Gamma pass rate was set to ≥ 95% as the success rate to quantify
the dosimetric accuracy of the investigated approaches. The first four
approaches presented unacceptable results going from 78% and bellow, whereas
the heterogeneous density approach performed better with 99% pass rate.
Furthermore, dose differences within the target volume showed better results for
the latter approach compared to water and fat approaches, i.e., 0.13% compared
to -2.66% and 2.46%, respectively.
Authors stated that when using additional bulk densities, the dosimetric
accuracy improves. However, this approach cannot be considered fully based on
MRI alone for the reason that it depends on CT images to assign the electron
density of spinal bone. Karotki et al.
(22) assigned three bulk densities to the segmented bone, air cavities
and air (1.5g/cm3, 0g/cm3, and 1g/cm3, respectively). Nevertheless, these
approaches suffer from segmentation errors and the required time for
segmentation is significantly extended.
Aside from the above-mentioned methods, more
sophisticated approaches are developed in order to assign the ED information to
MRI data which is the interest of this paper. We review and classify methods
for generating pseudo-CT images from MRI data. A classification of these
methods with a detailed description of research works involved in each class of
methods and some statistical performance results are presented. Nonetheless,
one cannot make a direct comparison between these approaches in the absence of
a generalised benchmark because of differences in the considered body region,
datasets, MRI sequence parameters, applied RT and types of performance metrics
used to evaluate the approach. We further address the advantages and drawbacks
of each class of methods and discuss new orientations to deal with the
limitation and difficulties encountered.
2. Performance metrics
To evaluate the performance of a certain
method for creating a pseudo-CT from MRI, the generated pseudo-CT is compared
to the gold standard CT (generally a real CT) using different performance
measures. We grouped evaluation measures to geometric and dosimetric measures. The
current section presents the common metrics used for evaluation.
1.1.
Geometric evaluation
measures
Measures in this category evaluate the
voxel-wise differences between the original and pseudo-CT in HU values. We find
the Mean Absolute Error (MAE) and the Mean Error (ME). Their respective
equations are given by:
![]()
and
![]()
Where N is the number of voxels, CTi andpseudoCTi are the HU value of a voxel at index iin the gold standard CT and the pseudo-CT, respectively.
The Dice Similarity Coefficient (DSC) for bone
(24) is a metric that measures the overlap between the original CT and the
pseudo-CT bone volumes. It is given by the
following formula:
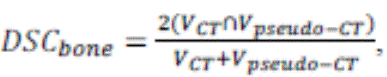
Where V
is the bone volume in the original CT and pseudo-CT.
1.2.
Dosimetric
evaluation measures
Metrics in this category
evaluate the dose differences of the generated plans between the original CT
and the pseudo-CT. One common metric is the gamma index γ (25) that evaluates
the dose distribution differences between each voxel in the original CT and the
pseudo-CT.
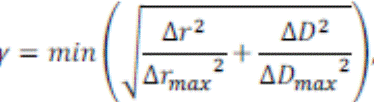
Where ![]() and
and ![]() are respectively
distance and dose between a voxel of interest and a neighbouring voxel in two
dose distributions.
are respectively
distance and dose between a voxel of interest and a neighbouring voxel in two
dose distributions. ![]()
![]() and
and![]() are the defined success thresholds. Generally, they
are set to these values
are the defined success thresholds. Generally, they
are set to these values![]() : and
: and ![]() of the prescribed dose.
of the prescribed dose.
The Dose Volume Histogram
(DVH) compares dose distributions, which expresses the minimal dose (DV) that a volume V (expressed in percent) receives. For
example, D98 is the minimal dose delivered to 98% of the volume of
interest. Probably add other measures without explanation
3. Classification of pseudo-CT
generation methods
The existing work in
deriving a pseudo-CT from MR images can be
broadly classified into four categories: segmentation-based,
intensity-based, atlas-based and hybrid methods. This latter consists of
approaches combining methods of the earlier categories. The choice of this
classification scheme was based on
considering the general technique applied in the approach. Other
classifications exist, where three categories are established, each grouping segmentation-based,
atlas-based and hybrid approaches (26). We preferred to make a broad categorizationin order to give a more
understanding of the methods. Figure 3 presents a diagram describing the
classification with some underlying techniques. This section provides a
detailed overview of each class with related works classified chronologically.
In this paper, the term pseudo-CT is used to refer to the MR image assigned ED
information.
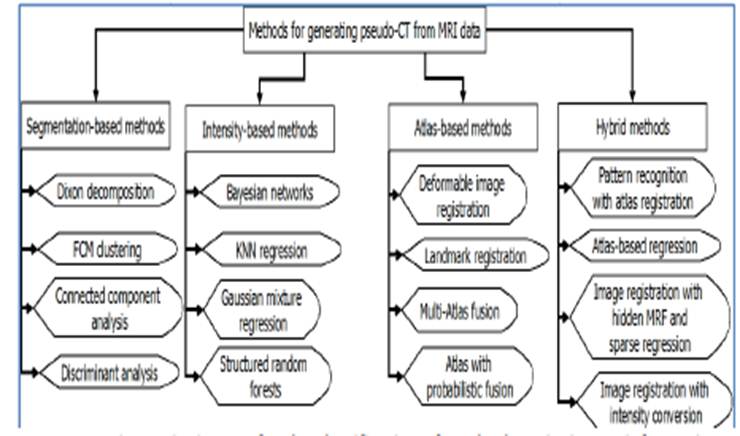
Figure .3 Diagram for the classification of methods
assigning ED information to MR images with some underlying techniques.
3.1.
Segmentation-based
approaches
These approaches rely on
segmenting MR images into several tissue classes: usually three, 4 or 5
classes, for example, bone, air, soft tissue and fat, based on Dixon sequences
(27-30), or using fuzzy logic algorithms (31, 32, 27, 33, 34). Then, each
tissue class is assigned a specific HU value in order to obtain the final
pseudo-CT.
Zaidi et al. (31) presented an MR segmentation approach
for attenuation and scatter correction in
a 3D Positron Emission Tomography (PET) by generating a patient-specific
attenuation map. After extraction of the skull and scalp on T1-weighted MR
images, they were registered to their corresponding reconstructed 3D PET
images, followed by recording spatial information from the registered maps.
This information was applied to the
original MR images that were segmented using a fuzzy C-means algorithm to yield
four tissue classes. Each class was assigned attenuation coefficients to obtain
the final MR segmented attenuation map. Qualitative and
quantitative results show an improvement compared to the clinical 3D brain PET
reconstruction using attenuation and scatter correction guided by measured
transmission. However, this approach follows many processing steps, which may
introduce a long processing time. Moreover, the accuracy of the MR-PET
registration depends on the used method and may introduce some registration
errors. In addition, the intensity
inhomogeneity artifacts present in the MR
images introduced a shading effect after the segmentation process. This latter
needed some manual interventions from the operator.
In (35), Boettger et
al. used two sets of MR images namely:
UTE sequence to enhance visualisation of
bony structures and an enhanced contrast sequence for soft tissue visualisation. The first data set of MR images
comprised of two sequences, one with an Ultrashort Echo Time pulse (UTE1) and
the other with a longer TE pulse (UTE2).
The second sequence (UTE2) was auto-segmented for skin detection; pixel
intensity values of this sequence were subtracted from the first sequence
(UTE1) to improve bone visualisation.
Moreover, They generated Digitally Reconstructed Radiographs (DDRs) based on a
look-up table that maps MR intensities to electron density values using
predefined thresholds. Furthermore, a pseudo-CT was
generated by assigning HU values to each tissue class (air, bone and soft tissue). The limitation of this
approach is that the bone segmentation technique can be used only on UTE
sequences. Moreover, this technique showed undesired results of over-segmenting
and under-segmenting partial regions of the brain.
Berker et al. (27) presented a four-class tissue
segmentation approach for MRI-based
attenuation correction. The MR images used are a UTE triple echo sequences
where the cortical bone segmentation is achieved
by using a dual echo technique (36). Soft tissue and adipose tissues were
segmented using a Dixon decomposition (28, 29), then the attenuation
coefficients are assigned to each tissue class. The approach presented a
misclassification between bone and soft tissue voxels.
In (32), authors presented
a classification approach to generate a pseudo-CT from several MR images such
as T1-weighted, T2-weighted, and two echoes from an Ultra-short Echo Time (UTE)
sequence. Next, fat and water images were calculated using a Dixon method.
These images were used to distinguish the major
tissue types of bone, fat, solid tissue, fluid and
air. The MR images were aligned together and
then a fuzzy c-means classification was performed in order to identify regions of interest and classify tissues. Each
tissue class was assigned a fuzzy membership probability and an appropriate
attenuation property. The final pseudo-CT is generated by summing attenuation
properties of each voxel. However, results show that the classifier tended to
misclassify air as bone and the use of UTE sequences does not completely separate bone from the air.
In (37), Rank et al.
presented a classification approach using discriminant analysis to derive a
pseudo-CT from different MR contrasts. The MR images were resampled to CT resolution with linear interpolation and then, each MR image was co-registered to
its corresponding CT with rigid registration taking mutual information as a
similarity measure. A threshold mask was used to limit the area of interest and
cross-validation was performed for
parameter optimisation. The optimisation resulted in TSE1 and UTE1
sequences as the best MR contrast combination with two features used (box.sd: the standard deviation of the
surrounding box including the central voxel multiplied by the intensity of the
voxel and dist.center: the
absolute distance of the voxel to the centre
of the 2D slice).Discriminant analysis is employed to assign observation
variable vectors composed of MR intensities features of a given voxel to
predefined classes using decision rules obtained in the learning step. Each CT
class is a 35 HU rang in the CT scale. Results showed a MAE of 81 HU, 95.2 HU and 90.1 HU for each phantom used,
respectively. The standard deviations of the absolute error between voxels were
in the range of 130 to 152 HU, which is a significantly large interval. For Ion
Radiotherapy Treatment (IRT) plan simulation, mean doses of the Planning Target
Volume (PTV) were 1.4-3.1% higher and volumes with PTV doses less than 90% of
the prescribed doses were 2.2-8.3% smaller compared to the original CT based
dose planning calculations.
Navalpakkam et al. (38) used UTE and 3D Dixon-VIBE sequences to
predict pseudo-CT images to be used for
the generation of µ-maps for MRI-based brain attenuation correction. The
process starts by performing a voxel-wise addition of UTE-TE1 (used for bone
identification), 3D-Dixon VIBE in-phase and 3D-Dixon VIBE out-phase images. The
resulting image was used to identify air regions by applying the k-means
clustering algorithm. To learn the relations between these processed images and
their corresponding CT images. Five patients were integrated into the learning
phase and support vector regression was used. Next, the generated regression
model was applied to five new MR patients to predict their pseudo-CT images.
Their approach gave a MAE of 2.4% with a Standard Deviation (SD) of 3.68% in
PET quantification for the whole brain.
Su et al. (30) proposed a method for acquisition, correction and generation of a
pseudo-CT image based on a single acquisition under-sampled UTE-m Dixon pulse
sequence. Two point Dixon volumes were reconstructed to provide water and fat
images. These images were used along aside with R* images, which provide bone
information as inputs for an unsupervised clustering algorithm to estimate five
tissue classes namely: air, brain, fat, fluid and bone, each class was assigned
a specific HU value to yield the final pseudo-CT. The mean absolute prediction
deviation between the gold standard (low dose CT) and the pseudo-CT was 130±16
HU and the mean prediction deviation was -22±29 HU.
Khateri et al. (33) used short-TE and two-point Dixon MR
sequences to generate µ-maps using Fuzzy C-means (FCM) algorithm focusing on
bone identification. Fat and water masks were derived from the in-phase, water,
and fat images using a modified C-means algorithm. The soft tissue mask was the
result of summing the air and water masks, this mask was applied to the
short-TE sequence. Later, this image was segmented based on a fuzzy C-means
algorithm yielding four tissue classes: bone, air, adipose tissue and soft
tissue; each of these classes belonging to a particular HU interval was assigned
attenuation values.
Liu et al. (39) employed T1 Dixon MR sequences in a classification scheme combined
with shape analysis to create a pseudo-CT. First, an initial mask was generated
by combining T1, water and fat images to detect bone and air voxels. Then, a
bone shape model (40) was applied to this mask in order to identify the pelvic
bone. Femur bone was detected using 3D connected component analysis. To segment
the rest of the body, a modified version of the FCM algorithm was applied and
five tissue classes were identified including compact bone, fat, muscle, and
the combination of fat interfaces and bone marrow. The pseudo-CT was generated
by assigning a specific HU value for each tissue class. MAE±SD was 274.9±26.9
HU for solid bone averaged on nine patients while muscle had an error of
13.7±1.8 HU.
Bredfeldt et al. (41) generated pseudo-CT images for the liver
using T1 Dixon MR sequences with FCM algorithm. The approach starts by
performing intensity thresholding on T1, water and fat images yielding an air
mask. In addition, the contours of the vertebral bone were segmented from the
fat images using a learning approach (42, 43). T1, water, and segmented fat
images were used as the input for a modified FCM algorithm (32) that resulted
in different tissue classes depending on their intensity (mid-intensity, lower
intensity, bone or marrow in the abdomen). The MAE ranged from 0 to 160
HU. However, the bone outside the
segmented anterior vertebra bodies was misclassified as mid and lower intensity
tissue. Nevertheless, this misclassification does not seem to affect the dose
calculation very much where the absolute dose differences are within acceptable
ranges (Median ±0.17 Gray (Gy) and Max± 0.81 Gy).
3.2.
Intensity-based
approaches
Intensity-based approaches
assume a one-to-one correspondence between MR and CT voxels and characterize
their intensities into tissue classes that are assigned electron density values
(44-46). Additionally, machine learning algorithms are used to characterize the
relations between CT and MRI voxels (47, 48).
Johansson et al. (49, 50) used three MR sequences, namely:
T2-weighted 3D Spin Echo (SE) based sequence and two Ultra-short Echo Time
(UTE) sequences (The UTE sequences are used to enhance visualization of bone).
Their approach used a Gaussian mixture regression model to link the MR and CT
intensities by performing clustering on the whole dataset with voxels from all
tissues wherean intensity value characterizes each cluster. The pseudo-CT voxel
values are calculated based on the estimated regression model. Streak artefacts
in MR images caused the major differences between the original CT and the
pseudo-CT. Furthermore, despite the use of UTE sequences to differentiate air
and bone, their suggested approach had large deviations between the real CT and
the pseudo-CT that were located at the air-soft tissue and bone-soft tissue
interfaces. To address this problem, authors extended their work (51) by
incorporation of spatial information, namely: x,
y and z coordinates of
each voxel and the shortest distance from each voxel to the external contour of
the anatomy. Results show an improvement in complicated small structures, but
no improvement was found in the larger anatomical volumes.
In (52), Kapanen et al used a
T1/T2*-weighted 3D Gradient Echo (GE) MR sequence for pelvic bones. The
relations between MR intensities and HU values were expressed using a
polynomial model that is based on MR signal intensity and fitting parameters.
The voxels of the segmented bone structures were grouped into sixteen subgroups
based on their MR intensity values. The polynomial model was then applied to
each of these subgroups to convert the mean MR intensities to Hounsfield
values.
Kim et al. (53) presented a voxel-based weighted
summation approach for generating a pseudo-CT from four MR sequences (3D
T1-weighted Fast Field Echo (FFE) sequence, 3D T2-weighted Turbo Spin Echo
(TSE) sequence, 3D balanced Turbo Field Echo sequence (bTFE) and an inverse
intensity volumetric image) for prostate cancer patients. Authors manually
contoured bone on T2-weighted sequences and registered them to their
corresponding CT volumes using rigid registration. Each MR voxel intensity was
calculated using a weighted summation of the intensities of the corresponding
voxels of the four MR sequences. Weight optimization was performed to reduce
errors starting with random weights to generate an initial pseudo-CT and
optimizing by reducing the Euclidian distance of calculated voxel value
differences between the pseudo-CT and real CT over one thousand iterations. In
addition, the resulting optimized weights were used for the next pseudo-CT
generation. Average MAE was 74.3 ± 10.9 HU for nine subjects; errors were
located around bone contour borders. However, manual bone contouring may
introduce uncertainty and it is time-consuming.
Korhonen et al. (54) presented a dual HU conversion model for
deriving a pseudo-CT from MR sequences based on two conversion models. The
first model was used to convert soft tissue MR signals to HU values: the idea
is to mark Regions Of Interest (ROIs) on CT scans (100 ROI for each patient)
covering muscle, urine, fat, prostate and rectal wall. These ROIs were then
transferred to MR images via co-registration. The MR intensity scale was
divided into ranges, each describing signals from different tissues (muscle,
urine, fat, prostate and rectal wall) and each MR intensity value belonging to
a specific signal rang is converted to the corresponding HU value. The second
conversion model is for converting signals from the bone tissue; authors used
the approach in (52) with a patient-specific cut-off to improve the
representation of low-density signals because these can vary significantly
between patients. Average tissue differences between the pseudo-CT and real CT
ranged from -2 to 5 HU for soft tissue, and from 22 to 78 HU for bone. However,
the conversion model overestimated HU values for low electron density
structures, and the manual bone segmentation introduces a significant time.
Moreover, the approach required manual adjustments of the signal cut-off for
each patient, which is not practical.
Roy et al. (48) followed a Bayesian scheme to generate a
pseudo-CT from two UTE MR sequences, each voxel of the reference images (two
UTE sequences and one CT scan) and the subject data was represented by a
feature vector called a patch. The subject and reference patches represent a
local pattern of intensities that have been scaled to a similar intensity rang.
Once the pairs of CT and MRI for both subject and reference are linked using a
Gaussian distribution, the unknown CT patches for the subject are predicted and
combined through the use of Bayesian networks.
In (55), Zhong et al.
presented a new method that uses KNN regression with learned local descriptors
to predict a CT from T1- and T2- weighted MR sequences. The approach consisted
in extracting local compact descriptors for each region in the MR sequences;
learning the transformations using the supervised descriptor technique (56) and
predicting CT image using KNN regression; where, for each point x of a subject MR image, a local search
window centre is defined in the same location in the training CT-MR pairs. The
prediction of the pseudo-CT was done by searching the K-nearest neighbours of
each point descriptor in the test MR image, the result is k MR descriptors, by considering the
alignment property of the MR-CT pairs, the k
samples of the corresponding CT are obtained. The final pseudo-CT is generated
by performing a weighted average on the overlap CT patches. Another recent work
by Huynh et al (57), where authors used structured random forests and auto
context model to estimate a CT. Their method consists of partitioning each MR
image into sets of patches where each patch is characterized by four features
that are extracted at three levels (voxel level, sub-region level and whole
patch level) including spatial information. To learn the relations between MR
and CT patches, structured random forests are used to train the MR features.
The resulting forests are used to predict initial CT patches. An auto-context
model is employed to enhance the prediction of the CT. The previous CT patches
are trained for new sets of random forests that are improved using ensemble
model to yield the final CT predicted image.
3.3.
Atlas-based
approaches
The approaches in this
class consist of using deformable registration algorithms (58-65) and a
database of aligned CT-MR atlases. The MRI atlas is warped to a target MR image
in order to capture the target’s anatomy. Then the resulting registration
transformations are applied to the CT atlas to predict the final pseudo-CT
image.
Kops et al. (66) followed a template-based scheme to
create PET transmission images from MR sequences. Ten PET transmission scans
were spatially normalized to the attenuation template of SPM2 (an SPM template
is composed of a pair consisting of a PET transmission scan and its
corresponding MR image), and averaged to create the transmission template. Each
subject’s MR and PET images were manually co-registered; then, the SMP2 MR
template was spatially normalized to the co-registered MR image. The resulting
transformation matrix is applied to the attenuation template to match the
subject’s anatomy.
Schreibmann et al. (67) used deformable image registration to
create a pseudo-CT from MR images. The idea is to warp an atlas CT image to the
patient MR image combining a parametric and non-parametric registration
algorithms namely B-Spline and Hermosillo, respectively. B-Spline was used to
account for large deformations while the Hermossilo algorithm was employed to
refine the results from the B-Spline registration. To evaluate their results,
authors used a three-dimensional surface comparison tool to compare the
differences between the pseudo-CT and the simulated CT (Gold standard). Test
results show that 20% of surfaces have an error larger than 2 mm and less than
1% of the surfaces presented errors larger than 1 cm for the bone.
Greer and al. (68) presented an MRI-based workflow for
radiation therapy, the subject’s MR image was automatically segmented by
registering it to an averaged set of manually segmented MR images used as an
atlas. A matching CT atlas set was used for an automatic estimation of electron
density values for each segment, therefore, mapping HU values to MR images.
Dowling et al. (69) presented an atlas-based electron density mapping method for
auto-segmentation of MR images and pseudo-CT generation. To construct the atlas
pair, a set of training MR-CT pairs was co-registered using rigid and affine
registration. The atlas MR image is generated by iteratively registering
training contoured MR images and averaging the results to obtain the atlas. The
transformation metrics and deformation fields from the previous registration
task are applied to the CT training set to generate the CT atlas. In order to
estimate the pseudo-CT, the new patients MR image is registered to the atlas MR
image for auto-segmentation, then the same deformations are applied to the CT
atlas.
In (17), authors used atlas
registration between T1-weighted MR images and a template patient composed of
matched pairs of CT-MR images to determine the geometry of each voxel
(position) given its intensity in the T1 MR image. This information is
represented by a Conditional Probability Function (PDF) and is combined into a
unifying posterior PDF. This PDF is used to predict the unknown electron
density values for the corresponding MR image.
Burgos et al. (70) proposed a multi-atlas scheme to
synthetize a CT and attenuation maps. They used a set of atlas images composed
of T1-weighted MR and CT scans. The first step aims at registering atlas images
to the target MRI using symmetric global registration and B-spline parametrized
non-rigid registration. Two morphological similarity measure were used: The
Local Normalized Correlation Coefficient (LNCC) and the local Normalized Sum of
Square Differences (NSSD). A ranking scheme was used to assign weights to the
registered images, i.e., the better is the registration, and the higher is the
weight. This step was followed by mapping the atlas CT scans to the
transformation maps obtained in the previous step using the assigned weights to
construct the target CT. However, the performance of this approach is limited
by the anatomical information of CT scans and T1-weighted MR sequences and
seems susceptible to the choice of optimization parameters.
Uh et al. (71) used atlas registration to create a pseudo-CT using T2-weighted
Turbo Spin Echo (TSE) MR sequences based on multiple atlas images. The atlas
set was composed of six pairs of MR-CT volumes that were registered with linear
rigid-body registration. Atlas MR volumes were later registered to the patient
MR volume using non-linear spatial registration. Then, the same deformations
are applied to the atlas CT volumes. To generate the pseudo-CT, authors used
three schemes to combine the deformed CTs, namely: arithmetic mean of each
voxel in each of the deformed CTs (Mean6), pattern recognition with Gaussian
process on 6 atlases, and on 12 atlases (PRGP6 and PRGP12). The intensity value
of each voxel is a weighted average of the corresponding voxels of the deformed
CTs. Results show that the generated pseudo-CT through PRGP12 performed better
in terms of the Root Mean Square (RMS) difference compared to the real CT (207
HU compared to 219 HU and 224 HU for PRGP6 and Mean6, respectively). Concerning
dose calculations, the D95 and the mean dose to the PTV results for
the three schemes differed from the original values by 1.8% and 1.3% of the
prescribed dose. The pseudo-CT generated with arithmetic mean showed the best
value of the volume satisfying the Chi-evaluation (98.7 compared to 98.3 and
98.5 for PRGP6 and PRGP12, respectively). However, all three used schemes
showed a smoothing effect where the high intensities in bone smear into the
surrounding tissue. Moreover, the Gaussian process scheme is computationally
expensive.
In (72), Sjölund et al proposedan
atlas-based regression technique to derive a pseudo-CT from T1-weighted MR
sequences. MRI and CT atlases were aligned with rigid registration. Then, the
MR atlas volumes were warped to the target MR image using the deformable image
registration algorithm Morphon (73) and a binary mask. The Morphon algorithm is
based on estimating displacement vectors that point to the corresponding
location in the target image. It uses local phase differences between signals
of similar local frequency to estimate the spatial shift. This is done based on
quadrature filters. The registration was performed on different scales to capture
large global displacements and small local deformations. The resulting
deformations were then applied to the atlas CT scans. The pseudo-CT was created
by fusing the deformed atlases by iteratively registering the set to its joint
mean.
Mérida et al. (74) presented a maximum probability approach
to generate a pseudo-CT from T1-weighted MR sequences. Their maximum
probability approach starts by registering atlas MRI to the target MRI volume.
The transformations from this registration were warped to the atlas CT scans to
deform them. For each voxel of these deformed CT volumes, a maximum probability
class label was calculated considering three tissue classes (soft tissue, air,
and bone) and the final voxel value is calculated by averaging HU values
belonging to the maximum probability class of the corresponding voxels in all
the deformed CT images.
In a more recent work,
Arabi et al. (75) presented a two-step atlas method focusing on bone tissue
identification. The first step aims at segmenting the target image in order to
identify bone structures based on a voxel by voxel voting scheme; the result is
a binary bone map. In the second step, a similarity measure is established
between atlas CT images and the resulting bone map in order to define weights
for the contribution of each CT atlas. An atlas fusion framework is locally
optimized according to the resemblance to the obtained target bone map and the
morphological similarity to the target MR volume.
Kraus et al. (76) used landmark image registration to predict
a pseudo-CT based on a rigidly registered pair of MR and CT images. The Atlas
MR image was registered to the target MRI using a marker-based rigid and
deformable registration. This transformation is applied to the atlas CT to
result in the pseudo-CT. MAE±SD ranged from 29.9±53.8 HU to 37.6±82.6 HU for
the body and from 31.3±27.3 HU to 37.3±35.8 HU for the prostate.
3.4. Hybrid
approaches
Other works use
combinations of the above-described approaches to combine their strengths,
reduce their weaknesses and palliate for limitations, approaches in this class
are called hybrid (77, 78, 79, 44, 80, 81, 46, 82).
Hoffman et al. (78) combined atlas registration and pattern
recognition to predict a pseudo-CT for attenuation correction. The approach consists
of learning a model on a dataset of registered MR-CT atlases to define a
mapping from MR intensities to CT intensities. The first step consists of using
B-spline registration with mutual information as a similarity measure to
construct the MR-CT atlas database. Then the MR atlases are registered to the
test MR volume using spatial normalization and the same transformations are
applied to the CT atlases. These transformed atlases are used to extract pairs
of MR patches and their corresponding CT values at each voxel location. A
regression process that incorporates prior knowledge from the transformed
images and uses a kernel function to measure the degree of similarity between
MR patches was used to predict CT values for an unseen MR patch and generate the
final pseudo-CT. The approach overestimated the bone in case of the presence of
a proximate lesion.
Chen et al. (79) estimated a pseudo-CT from standard
T1-weighted MR sequences of the head taking into account distinction between
bone and air. To do this, authors generated air maps from CT scans and rigidly
registered them to the corresponding MR images. This was done for all the atlas
images of the training set, and then all air maps were warped to the patient MR
image to locate air, once this is done. For each air voxel, an average CT value
is assigned from atlas voxels of the same location. At tissue location, hidden
Markov Random Field (hMRF) and sparse regression were used to predict CT
values. The idea is to measure the resemblance between the MR atlas patches and
the patient MR patch to assign a high weight if the resemblance is strong,
assuming that similar MR patches correspond to similar CT patches. The final
value of the pseudo-CT patch is calculated using the weighted average of the
overlap CT atlas patches. Despite the good results in PET simulation;
1.60±0.51% for the Mean Absolute Relative Error (MARE) and 5.45± 1.36% for the
Full Width Tenth Maximum (FWTM), the approach presented some misclassification
results where some bone was classified as air. Furthermore; when compared with
the averaged atlas method, if one would choose a compromise between workload
and accuracy, the averaged atlas approach would be chosen since the presented
results are acceptable (1.70±0.57% for MARE and 6.3±1.29% for FWTM).
In (44), Andreasen et al presented a
patch-based approach for predicting pseudo-CT from conventional MR sequences.
Five brain images from MR and CT were aligned using mutual information as a
similarity measure (the aligned images constitute the patch database). Each
patch P(x) in an x MR location corresponds to a T(x) value defining an HU value in the
corresponding aligned CT scan. The pseudo-CT for the test patient is predicted
using an intensity-based nearest neighbour search in the patch database. For
each test patch, the goal is to find the minimized squared L2-norm between the test patch and the database of patches. K most similar CT patches are found and
the final CT patch value is obtained by computing a similarity-weighted
average. The structural similarity measure was used to discard the high
dissimilar patches and reduce the search space. This approach depends on
anatomical similarities, and the assignment of the average of the surrounding
patches can cause problems when the surrounding tissues are different from the
one being calculated.
Siversson et al. (80) used an automatic tissue classification
approach using statistical decomposition algorithm with image registration to
predict CT images for the pelvic region. A database of contoured MR-CT pairs is
used to register the atlas MR images to the patient’s MR image. Each pair
registration yields a candidate organ segmentation and the final MR
segmentation is calculated using a weighted voting method. Next, a non-linear
warping procedure is applied to each of the atlas MR images in order to align
the segmented structures to the newly segmented MR image. The resulting
deformation fields are applied to their corresponding CTs and the final
pseudo-CT is generated by fusing all the deformed CTs. Mean absorbed dose
differences to the target was 0.0%±0.2 (1.s.d) and the MAE was 36±4.1 (1.s.d)
within the body contour.
Wu et al. (46) used local sparse correspondence
combination to predict a pseudo-CT for the head. They assumed that MR and CT
patches (each patch is a feature vector) are located on two non-linear
manifolds. The approach consists of constructing initial MR and CT patch
dictionaries by collecting patches within a local search window, next, the Knnalgorithm is applied to restrict the number
of patches in the dictionaries. The MR dictionary is used to linearly represent
the MR testing sample while ensuring the locality of the representation. The
final CT patches are predicted by doing a weighted average of the corresponding
CT patches.
Demol et al. (82) introduced an approach that uses
deformable image registration combined with MR intensity information to
generate a pseudo-CT from T1-weighted MR images of the brain. This approach
aims at incorporating the MR intensity values into the generation of the
pseudo-CT. The approach starts by registering an atlas MR image to its
corresponding CT image via rigid registration with mutual information as a
similarity measure. Then, the atlas MR image is non-rigidly registered to the
MR image of the patient using the hybrid deformable image registration
algorithm ANACONDA. The same deformations are applied to the CT atlas. Later,
these two deformed atlas images were resampled to the same coordinate grid to
apply voxel intensity computations. I.e., in the deformed MR image, a certain
group of similar voxels was selected by doing a local search inside a 9×9×9 box
centred at each voxel with the selection threshold set to 10%. The pseudo-CT
value is calculated by averaging the CT values at the corresponding voxel
location of the deformed CT. Comparison with the real CT resulted in an MAE of
150 HU. The main limitation of the approach is that the MR intensity search
introduced incoherent CT numbers due to increasing the search area when no
corresponding voxels are found inside the search box. Furthermore, noise near
bone and air cavities was detected.
A recent work of Burgos et
al. (81) used a database containing
delineated T1, T2, CT images and a manually segmented image to create a
pseudo-CT by combining atlas registration with segmentation in a single
iterative framework. First, the atlas T1 and T2 images are registered to the
target MR image to obtain an initial segmentation, and the transformations are
applied to the atlas CT images to obtain an initial pseudo-CT. The initial segmentation and pseudo-CT are
used alongside with the atlas database as inputs for the next iteration, and
the process is repeated until satisfactory results are obtained. The number of
iterations was set to four and the registration was based on two similarity
measures, namely: the Structural Similarity Extended to Irregular Regions of
Interest (ROI-SSIM) (83), and the Local Similarity Measure (LSIM). The DSC was
calculated to evaluate segmentation results, and values ranged from 0.73 to 0.9
for prostate, bladder, rectum and femur heads. The MAE±SD was 45.7±4.6 HU, and
the average difference of D98 in the PTV was -0.14%.
4. Discussion
Tables 1, 2, 3 and 4 represent the classification
of methods with the datasets, body regions, MR sequences and some numeric
results of pseudo-CT images generated using several methods. From the tables,
It is clear that most of the research focused primarily on the brain and
secondly on the pelvis regions whereas poor work concentrated on the liver. The
MAE ranged from 80 HU to 137 HU and from 36.4 HU to 74 HU for the brain and
pelvis, respectively, which are within acceptable ranges.
The use of more specialized MR sequences does not
seem to improve results remarkably except having the bone visualization feature
as a bonus. In addition, we notice a recent increasing interest in the Dixon MR
sequence since it has the advantage of producing multiple contrast images with
a single acquisition. As well as the incorporation of segmentation techniques
which is taking place to account for different tissues present in the body.
Despite the clinically acceptable performance
results of these approaches. Each class of methods presents some drawbacks and
limitations that should be taken into consideration and could extend the field
of research in MRI-only RT. Approaches that are based on using segmentation algorithms
suffer from segmentation errors, which can result in a misclassification of
voxels. Moreover, the bone is often ignored because the standard MR sequences do
not show any signal from the bone. Some research has investigated the use of
other more specialized MR sequences that are capable of detecting signals from
the bone using two Times of Echo (TE) after the radio frequency (RF)
excitation. This type of sequence is called Ultra-short Echo Times sequences
(UTE) (85, 49, 27, 86, 87, 88, 89, 90, 33). It relies on measuring early
relaxation signals from cortical bone structures. Another specialized MR
sequence for detecting the bone signal is Zero-Echo Time imaging (ZTE) (91,
92). Delso et al. (91) showed that the bone segmentation using
ZTE sequences performed better than the UTE-Based segmentation. However, these
techniques are limited by their expensive implementation requirements and long
acquisition time. Furthermore, whole body UTE imaging results in increased
noises because of the short relaxation times of the cortical bone (93).
Other attempts
to detect the bone combined Short-TE sequences with Dixon pulse sequences in a fuzzy
C-means framework to determine tissue classes including cortical bone (94, 33,
34). Techniques incorporating machine learning
schemes to segment the bone seem very promising; Bredfeldt et al. (41) segmented the contours of the vertebra bone from fat images using a
learning approach (43, 42) and Liu et al. (39)
applied a bone shape model to detect the pelvic bone; in addition, Femur bone
was detected using 3D connected component analysis.
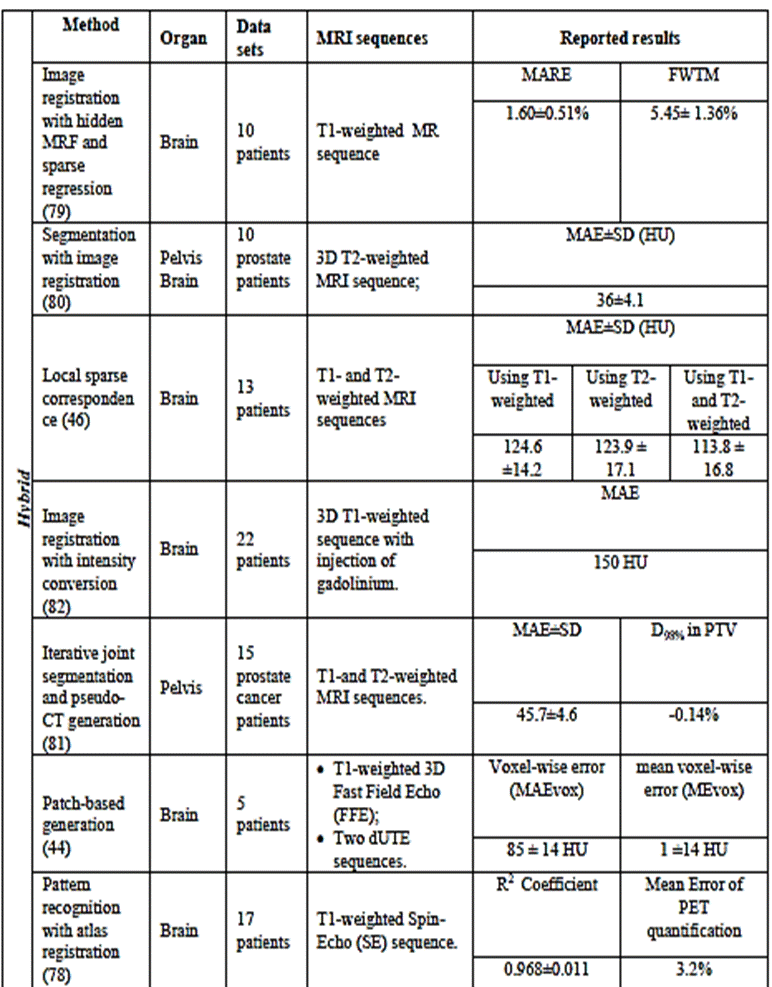
Table
1.
Intensity-based approaches for generating
pseudo-CT from MRI data.
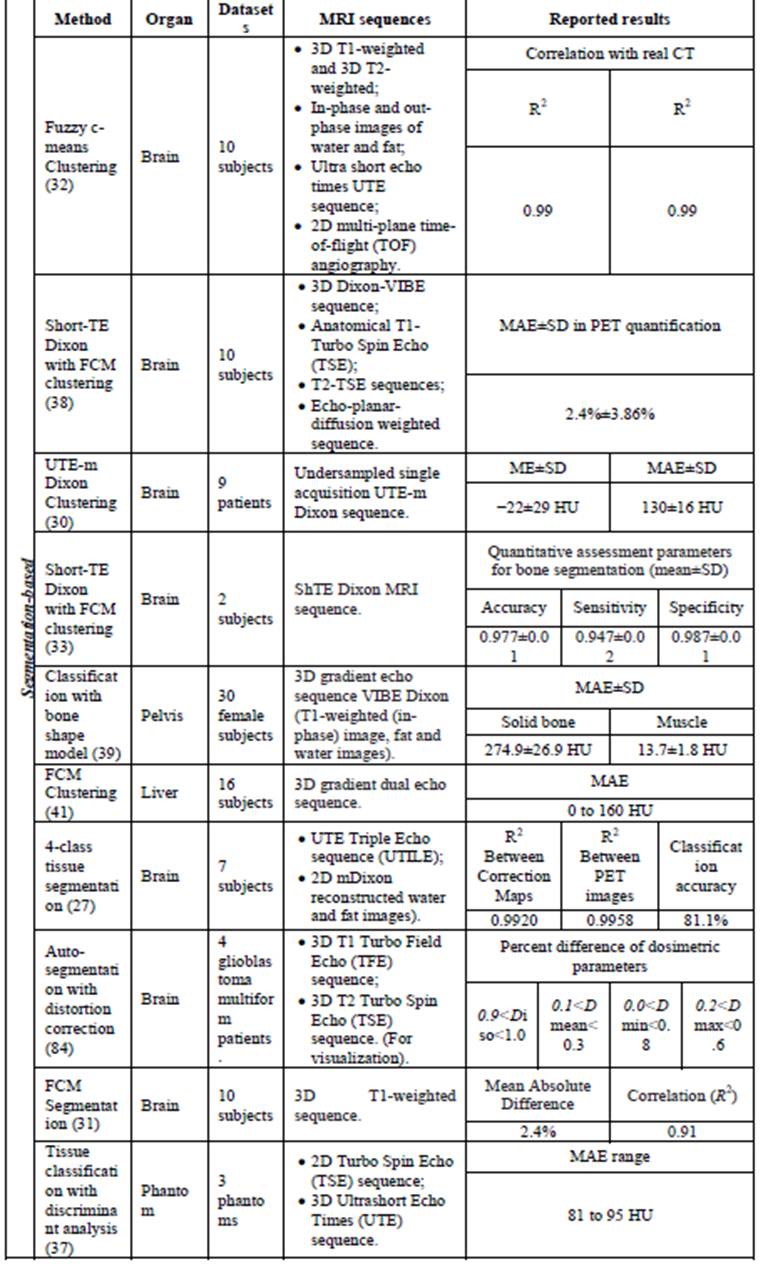
Table
2.
Segmentation-based approaches for generating pseudo-CT from MRI data.
|
Atlas-based |
Method |
Organ |
Datasets |
MRI
sequences |
Reported
results |
|||||||
|
Atlas fusion
and segmentation (75) |
Pelvis |
12 patients
with loco-regionally advanced rectal cancer |
MRI
Dixon volumetric interpolated T1-weighted sequence. |
Mean ± SD (Absolute mean ± SD) |
||||||||
|
Fat |
Soft-tissue |
Bone |
||||||||||
|
2.2 ± 5.5 (5.6 ± 4.5) |
−2.0 ± 4.1 (5.0 ± 3.9) |
−1.5±5.0 (4.1±2.2) |
||||||||||
|
Multi-atlas
information propagation (70) |
Brain |
12 patients
(optimisation) 41 patients
(validation) |
T1-weighted
MR sequence. |
Average MAE±SD |
Average ME±SD |
|||||||
|
121±17 HU |
-7.3±23 HU |
|||||||||||
|
Electron
density mapping for MRI (69) |
Pelvis |
37 patients
with prostate cancer |
· T2
fast spin echo FSE sequence; · T2* gradient echo
sequence; · Whole pelvic fast spin
echo FSE sequence. |
Mean ± SD (HU) |
||||||||
|
Rectum |
Bladder |
Bone |
prostate |
|||||||||
|
54 ±143 |
9 ±6 |
340 ±85 |
42 ±25 |
|||||||||
|
Unifying
probabilistic fusion (17) |
Brain |
9 patient with
brain tumour |
T1-weighted
rapid gradient echo sequence. |
MAE± SD |
Accuracy |
|||||||
|
126±25 HU |
86.6% |
|||||||||||
|
Atlas
registration with fusion (71) |
Brain |
26 patient
with paediatric brain tumour |
T2-weighted
Turbo Spin-Echo (T2 TSE) prior to the injection of contrast agent. |
RMSD±SD |
Correlation coefficient |
|||||||
|
MEAN6 |
MEAN12 |
PRGP12 |
MEAN6 |
MEAN12 |
PRGP12 |
|||||||
|
224±36 HU |
219±35 HU |
207±33 HU |
0.787±0.06 |
0.798±0.059 |
0.819±0.058 |
|||||||
|
Template-based
(66) |
Brain |
4 patients |
High-resolution
3D T1 weighted volumetric MR using MP-RAGE sequence. |
Overestimation of the
reconstructed radioactivity up to 9% |
||||||||
|
Combined
deformable registration (67) |
Brain |
17 brain
tumour patients |
/ |
Mean distance |
Mean HU differences |
|||||||
|
External contour |
Bony anatomy |
< 2 HU |
||||||||||
|
1,26 mm |
2.15 mm |
|||||||||||
|
Segmentation
and pseudo-CT generation (68) |
Pelvis |
39 patients with
prostate cancer |
T2-weighted
MR sequence |
Paired t-test |
||||||||
|
>0.09 |
||||||||||||
|
Maximum
probability Multi-Atlas (74) |
Brain |
27 patients |
T1-weighted
MR sequence |
Voxel classification
error |
||||||||
|
7.81% ± 1.00% |
||||||||||||
|
Landmark image
registration (76) |
Phantom |
Phantom |
T2-weighted
MR sequence |
MAE±SD (prostate) |
||||||||
|
31.3±27.3 HU to 37.3±35.8 HU |
||||||||||||
|
Atlas-based
regression (72) |
Brain |
10 patients |
T1-weighted
3D spoiled gradient recalled echo sequence |
MAE ± SD |
||||||||
|
113.4±17.6 HU |
||||||||||||
Table
3.
Atlas-based approaches for generating pseudo-CT from MRI data.
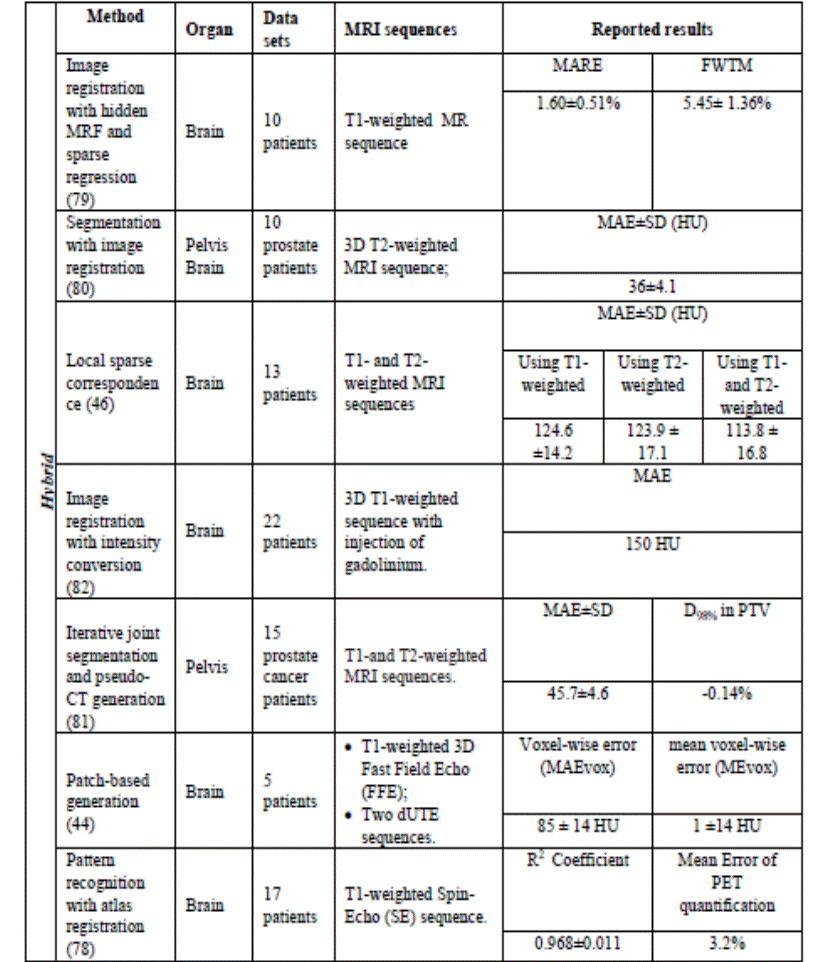
Table 4.Hybrid approaches for generating pseudo-CT from MRI
data.
Intensity-based approaches assume a direct link
between MR voxel values and CT values. However, this link cannot be characterised (78). This is because tissues like air and bone have different CT values
whereas they present no signal on MR images. Moreover, the use of machine
learning technique could be advantageous. Nevertheless, sufficient knowledge
must be incorporated to improve the prediction quality, but the training time
relatively increases with respect to the
increased size of required training data sets. Edmund et al. (45) investigated the geometric
and dosimetric performance of three intensity-based approaches using UTE MR
sequences, namely: threshold-based segmentation, Bayesian segmentation, and
statistical regression. In the threshold-based approach, thresholds are set
manually to define tissues based on inspection of MR intensities. Voxel values are assigned according to echo times TE1 and
TE2 intensities, and four classes of tissues were defined. The second approach is based on the Expectation Maximization(EM) algorithm, which estimates a
probability that each voxel belongs to a specific tissue class, and then voxels
are assigned to the class with the highest posterior probability. The
regression-based approach uses both MR and CT data to train a regression model
based on the EM algorithm that predicts a pseudo-CT for an untrained MR image. The investigation was performed on five patients; results show that the
regression-based approach gave the best results in
terms of geometric and dosimetric performances. Whereas, the other two
approaches did not show a good correlation between geometrical agreement.
Approaches that rely on deformable image
registration algorithms make the success of pseudo-CT generation related to the
accuracy of registration; moreover, image registration introduces geometric
uncertainties due to inter-patient variations and abnormalities. To assess the
quality of deformable registration, Schreibmann et al. (67) developed a three-dimensional surface comparison
tool that extracts a specific surface from the pseudo-CT and the simulated CT
(gold standard) to compare the differences. Demol et al. (82) studied a specific case in detail with the
aim of testing the performance of their proposed method (see subsection 3.4 for
details of the approach) with atypical body structures. The case studied had a
part of the skull bone removed surgically. The generated pseudo-CT presented additional bone in the location where the
patient’s MR image did not have any. Furthermore, the number of atlas images
used to generate the pseudo-CT should be carefully selected (95) and the acquired atlas dataset should be
representative of standard anatomy. The use of multi-atlas data fusion
techniques (74, 17, 71, 70, 75, 96, 69, 72, 97, 98) appears to give improved
results compared to the single atlas technique since the pseudo-CT values will be predicted from several CT atlas images.
Mérida et al. (74) evaluated four multi-Atlas methods for
pseudo-CT generation, their maximum probability approach (74) and three
multi-Atlas approaches; the first method is a multi-Atlas propagation and
fusion technique (70). The second is a best_10 approach where ten best-ranked
deformed CT atlases are fused using non-weighted average and the last approach consists of fusing all
deformed atlas CT images with a non-weighted average. Comparison results showed
that the best_10 method performed better giving small voxel classification
error 7.57 ± 1.05 compared to 7.95 ± 1.00, 7.81 ± 1.00 and 7.69 ± 1.04 for the
Average, Max probability and the multi-Atlas propagation and fusion methods
respectively.
Whelan et al. (99) evaluated the effect of electron density errors on dose
calculation for the cervix cancer. They generated four pseudo-CT images using
four methods: Atlas (100), homogenous
bulk density assignment (16), rigid registration (101, 102) and bone bulk
density (16). Comparison results show that the largest
errors were observed for the bone density method when the bone is assigned the
value of 1.21 g/cm3 concluding that a wrong assignment of
electron density values can result in dose changes when compared to the dose
calculated on the gold standard CT.
One concern that should be considered is geometric distortions related
to non-linearity in spatial encoding gradients and chemical shift distortions
caused by susceptibility effects. The quality of the generated pseudo-CT could
be affected negatively if the used MR sequences contain distortions. Many research papers presented techniques to
correct for geometric distortion (103) and chemical shift (104). In this scope, Stanescu et al. (84) investigated on the effect of distortion correction of MR images
on dose calculation. The corrected MR images were auto-segmented to define head
structures (scalp, bone,and brain). Bulk
CT values were assigned to these
segmented regions. The dose calculations generated on these images ware
compared to those generated by the conventional MRI-CT workflow. Percentual differences of the mean dose
differences ranged from 0.2 % to 0.3 % for four patients. Beavis et al. (13) proved that it is possible to perform MRI-only RT by using a small
field of view, an increased receiver bandwidth and a fast spin echo acquisition
sequence.
The reported results for
most of the above-mentioned research
works are in acceptable ranges and confirm the success of pseudo-CT in
replacing the original CT in RT. This
field of research is emerging towards the use of MRI as the only modality in RT
especially with the introduction of hybrid PET/MR systems for attenuation
correction and it is opening research opportunities to improve the field of
MRI-alone RT.
5. Conclusion
This paper
aimed to review approaches for pseudo-CT generation from MR images for an
MRI-only radiotherapy treatment workflow. We presented a classification of
these approaches, discussed their strengths and weaknesses and covered some
possible solutions and future orientations. Lately, research is oriented towards including specialised MRI sequences such as UTE and ZTE
despite their complex implementation. Furthermore, new approaches and
techniques are being integrated to deal with the bone visualisation issues. We notice that techniques that follow a
segmentation scheme are being more established for the success brought by new
segmentation algorithms that are implemented based on novel algorithms using
deep learning or machine learning methods. We conclude that the quality of the
generated pseudo-CT depends strongly on the applied approach and the used MR
sequences. Although many approaches seem promising, one cannot choose the best
method compared to the others; this is because different MR sequences,
parameters, datasets and test metrics are used to generate the pseudo-CT and
assess its quality. Hence, a benchmark is needed to set in common performance metrics.
6. Authors biography
Ms. Wafa Boukellouzis currently a Ph.D. student in
Computer Science - University of Ferhat Abbas, Setif, Algeria. She obtained her
Master’s degree in 2015 from M’HamedBouguerra University, Boumerdes,
Algeria. Currently, she is working in the field of intelligent systems
engineering. Her main research interests
include medical image processing and machine learning.
Pr. Abdelouahab Moussaoui is a professor at
the department of informatics, University of Ferhat Abbas, Setif, Algeria. His research interests are in the areas of data mining
and machine learning (knowledge discovery, clustering, classification, etc.),
signal and medical imaging (RMN, FMRN, PET, Mammography, ECG, EEG, etc.),
bioinformatics and bio-mining (Pattern search, alignment of sequences,
structure prediction, etc.), soft-computing and bio-inspired algorithms (Neural
networks, GA, PSO, Artificial Ants, etc.)
7. Conflicts of interest
This paper is a revised and
an expanded version of a paper entitled ‘Classification of methods for
generating pseudo-CT images for MRI-alone RT’ presented at the International
Workshop on Medical Technologies 2017 co-located with ICHSMT 2017, Tlemcen,
Algeria, 10-12 October 2017 (23).
8.References
1. O'Neill, B., Salerno, G.,
Thomas, K., Tait, D. and Brown, G. (2009). MR vs
CT imaging: low rectal cancer tumour delineation for three-dimensional
conformal radiotherapy. The British Journal
of Radiology, [online] 82(978), pp.509-513. Available at: http://dx.doi.org/10.1259/bjr/60198873. [Accessed 8 Jun.
2017].
2. Rasch, C., Barillot, I.,
Remeijer, P., Touw, A., van Herk, M. and Lebesque, J. (1999). Definition of the
prostate in CT and MRI: a multi-observer study. International Journal of Radiation Oncology*Biology*Physics,
[online] 43(1), pp.57-66. Available at: http://dx.doi.org/10.1016/s0360-3016(98)00351-4. [Accessed 8 Jun.
2017].
3. Moser, E., Stadlbauer, A.,
Windischberger, A., Quick, H H., Ladd, M E., (2009). Magnetic resonance imaging
methodology. European Journal of Nuclear
Medicine and Molecular Imaging. [online]
36(1):30. Available at: http://dx.doi.org/10.1007/s00259-008-0938-3.
4.
Chao, M., Xie, Y. and Xing, L. (2008). Auto-propagation of contours for
adaptive prostate radiation therapy. Physics
in Medicine and Biology, [online] 53(17), pp.4533-4542. Available at: http://dx.doi.org/10.1088/0031-9155/53/17/005. [Accessed 8 Jun. 2017].
5.
Thor, M., Petersen, J., Bentzen, L., Høyer, M. and Muren, L. (2011).
Deformable image registration for contour propagation from CT to cone-beam CT
scans in radiotherapy of prostate cancer. ActaOncologica,
[online] 50(6), pp.918-925. Available at: http://dx.doi.org/10.3109/0284186x.2011.577806. [Accessed
8 Jun. 2017].
6.
Thörnqvist, S., Petersen, J., Høyer, M., Bentzen, L. and Muren, L.
(2010). Propagation of target and organ at risk contours in radiotherapy of
prostate cancer using deformable image registration. ActaOncologica, [online] 49(7), pp.1023-1032. Available at: http://dx.doi.org/10.3109/0284186x.2010.503662. [Accessed 8 Jun.
2017].
7.
Van der Put, R., Kerkhof, E., Raaymakers, B., Jürgenliemk-Schulz, I. and
Lagendijk, J. (2009). Contour propagation in MRI-guided radiotherapy treatment
of cervical cancer: the accuracy of rigid, non-rigid and semi-automatic
registrations. Physics in Medicine and
Biology, [online] 54(23), pp.7135-7150. Available at: http://dx.doi.org/10.1088/0031-9155/54/23/007. [Accessed
8 Jun. 2017].
8.
Faggiano, E., Fiorino, C.,
Scalco, E., Broggi, S., Cattaneo, M., Maggiulli, E., Dell 'O ca, I., Di Muzio, N., Calandrino, R. and
Rizzo, G. (2011). An automatic contour propagation method to follow parotid gland
deformation during head-and-neck cancer tomotherapy. Physics in Medicine and Biology, [online] 56(3), pp.775-791.
Available at: http://dx.doi.org/10.1088/0031-9155/56/3/015. [Accessed
8 Jun. 2017].
9.
Commandeur,
F., Simon, A., Mathieu, R., Nassef, M., Ospina, J., Rolland, Y., Haigron, P.,
De Crevoisier, R. and Acosta, O. (2016). MRI to CT prostate registration for improved targeting in cancer
external beam radiotherapy. IEEE Journal of
Biomedical and Health Informatics, [online] pp.1-1. Available at: http://dx.doi.org/10.1109/jbhi.2016.2581881. [Accessed 8 Jun.
2017].
10. Cattaneo, G., Reni, M., Rizzo, G., Castellone, P., Ceresoli, G.,
Cozzarini, C., Ferreri, A., Passoni, P. and Calandrino, R. (2005). Target delineation in post-operative radiotherapy of brain gliomas:
Interobserver variability and impact of image registration of MR
(pre-operative) images on treatment planning CT scans. Radiotherapy and Oncology, [online] 75(2),
pp.217-223. Available at: http://dx.doi.org/10.1016/j.radonc.2005.03.012. [Accessed 8 Jun.
2017].
11. Nyholm, T., Nyberg, M.,
Karlsson, M. and Karlsson, M. (2009). Systematization of spatial uncertainties
for comparison between a MR and a CT-based radiotherapy workflow for prostate
treatments. Radiation Oncology,
[online] 4(1), p.54. Available at: http://dx.doi.org/10.1186/1748-717x-4-54. [Accessed
8 Jun. 2017].
12. Ulin, K., Urie, M. and
Cherlow, J. (2010). Results of a Multi-Institutional Benchmark Test for Cranial
CT/MR Image Registration. International
Journal of Radiation Oncology*Biology*Physics, [online] 77(5),
pp.1584-1589. Available at: http://dx.doi.org/10.1016/j.ijrobp.2009.10.017. [Accessed 8 Jun.
2017].
13. Beavis, A., Gibbs, P.,
Dealey, R. and Whitton, V. (1998). Radiotherapy treatment planning of brain
tumours using MRI alone. The British Journal
of Radiology, [online] 71(845), pp.544-548. Available at: http://dx.doi.org/10.1259/bjr.71.845.9691900. [Accessed 8 Jun.
2017].
14. Lee, Y. (2003).
Radiotherapy treatment planning of prostate cancer using magnetic resonance
imaging alone. Radiotherapy and Oncology,
[online] 66(2), pp.203-216. Available at: http://dx.doi.org/10.1016/s0167-8140(02)00440-1. [Accessed 8 Jun.
2017].
15. Jonsson, J., Karlsson, M.,
Karlsson, M. and Nyholm, T. (2010). Treatment planning using MRI data: an
analysis of the dose calculation accuracy for different treatment regions. Radiation Oncology, [online] 5(1), p.62.
Available at: http://dx.doi.org/10.1186/1748-717x-5-62. [Accessed 8 Jun. 2017].
16. Lambert, J., Greer, P.,
Menk, F., Patterson, J., Parker, J., Dahl, K., Gupta, S., Capp, A., Wratten,
C., Tang, C., Kumar, M., Dowling, J., Hauville, S., Hughes, C., Fisher, K.,
Lau, P., Denham, J. and Salvado, O. (2011). MRI-guided prostate radiation
therapy planning: Investigation of dosimetric accuracy of MRI-based dose
planning. Radiotherapy and Oncology,
[online] 98(3), pp.330-334. Available at: http://dx.doi.org/10.1016/j.radonc.2011.01.012. [Accessed 8 Jun.
2017].
17. Gudur, M., Hara, W., Le,
Q., Wang, L., Xing, L. and Li, R. (2014). A unifying probabilistic Bayesian
approach to derive electron density from MRI for radiation therapy treatment
planning. Physics in Medicine and Biology,
[online] 59(21), pp.6595-6606. Available at: http://dx.doi.org/10.1088/0031-9155/59/21/6595. [Accessed 8 Jun.
2017].
18. Chen, L., Price, R., Wang,
L., Li, J., Qin, L., McNeeley, S., Ma, C., Freedman, G. and Pollack, A. (2004).
MRI-based treatment planning for radiotherapy: Dosimetric verification for
prostate IMRT. International Journal of
Radiation Oncology*Biology*Physics, [online] 60(2), pp.636-647.
Available at: http://dx.doi.org/10.1016/j.ijrobp.2004.05.068. [Accessed 8 Jun.
2017].
19.
Eilertsen, K., Nilsen Tor Arne Vestad, L., Geier, O. and Skretting, A.
(2008). A simulation of MRI based dose calculations on the basis of
radiotherapy planning CT images. ActaOncologica,
[online] 47(7), pp.1294-1302. Available at: http://dx.doi.org/10.1080/02841860802256426. [Accessed 8 Jun. 2017].
20.
Pasquier,
D., Palos, G., Castelain, B., Lartigau, E. and Rousseau, J. (2004). MRI simulation for conformal radiation therapy of prostate cancer. International Journal of Radiation
Oncology*Biology*Physics, [online] 60(1), pp.S636-S637. Available
at: http://dx.doi.org/10.1016/j.ijrobp.2004.07.656. [Accessed 8 Jun. 2017].
21. Hoogcarspel,
S., Van der Velden, J., Lagendijk, J., van Vulpen, M. and Raaymakers, B.
(2014). The feasibility of utilizing pseudo CT-data for online MRI based
treatment plan adaptation for a stereotactic radiotherapy treatment of spinal
bone metastases. Physics in Medicine and
Biology, [online] 59(23), pp.7383-7391. Available at: http://dx.doi.org/10.1088/0031-9155/59/23/7383. [Accessed 8 Jun.
2017].
22. Karotki, A., Mah, K.,
Meijer, G. and Meltsner, M. (2011). Comparison of bulk electron density and
voxel-based electron density treatment planning. Journal of Applied Clinical Medical Physics, [online] 12(4),
pp.97-104. Available at: http://dx.doi.org/10.1120/jacmp.v12i4.3522. [Accessed 8 Jun.
2017].
23.
W. Boukellouz and A.
Moussaoui, Classification of methods
for generating pseudo-CT images for MRI-alone RT, Medical Technologies Journal, vol. 1, no. 3, pp.54-54. Sep. 2017. Available at: http://dx.doi.org/10.26415/2572-004X-vol1iss3p54-54. [Accessed 28 Feb. 2018].
24.
Dice, L. (1945). Measures of the Amount of Ecologic Association Between
Species. Ecology, [online] 26(3),
pp.297-302. Available at: http://dx.doi.org/10.2307/1932409. [Accessed 9 Jun. 2017].
25. Low, D., Harms, W., Mutic,
S. and Purdy, J. (1998). A technique for the quantitative evaluation of dose
distributions. Medical Physics,
[online] 25(5), pp.656-661. Available at: http://dx.doi.org/10.1118/1.598248. [Accessed 9 Jun. 2017].
26. Edmund, J. and Nyholm, T.
(2017). A review of substitute CT generation for MRI-only radiation therapy. Radiation Oncology, [online] 12(1).
Available at: http://dx.doi.org/10.1186/s13014-016-0747-y. [Accessed 8 Jun.
2017].
27. Berker, Y., Franke, J.,
Salomon, A., Palmowski, M., Donker, H., Temur, Y., Mottaghy, F., Kuhl, C.,
Izquierdo-Garcia, D., Fayad, Z., Kiessling, F. and Schulz, V. (2012). MRI-Based
Attenuation Correction for Hybrid PET/MRI Systems: A 4-Class Tissue
Segmentation Technique Using a Combined Ultrashort-Echo-Time/Dixon MRI
Sequence. Journal of Nuclear Medicine,
[online] 53(5), pp.796-804. Available at: http://dx.doi.org/10.2967/jnumed.111.092577. [Accessed 8 Jun.
2017].
28. Dixon, W. (1984). Simple
proton spectroscopic imaging. Radiology,
[online] 153(1), pp.189-194. Available at: http://dx.doi.org/10.1148/radiology.153.1.6089263. [Accessed 8 Jun. 2017].
29. Glover, G. and Schneider,
E. (1991). Three-point dixon technique for true water/fat decomposition with B0
inhomogeneity correction. Magnetic Resonance
in Medicine, [online] 18(2), pp.371-383. Available at: http://dx.doi.org/10.1002/mrm.1910180211. [Accessed 8 Jun.
2017].
30. Su, K., Hu, L., Stehning,
C., Helle, M., Qian, P., Thompson, C., Pereira, G., Jordan, D., Herrmann, K.,
Traughber, M., Muzic, R. and Traughber, B. (2015). Generation of brain
pseudo-CTs using an undersampled, single-acquisition UTE-mDixon pulse sequence
and unsupervised clustering. Medical Physics,
[online] 42(8), pp.4974-4986. Available at: http://dx.doi.org/10.1118/1.4926756. [Accessed 8 Jun.
2017].
31. Zaidi, H., Montandon, M.
and Slosman, D. (2003). Magnetic resonance imaging-guided attenuation and
scatter corrections in three-dimensional brain positron emission tomography. Medical Physics, [online] 30(5),
pp.937-948. Available at: http://dx.doi.org/10.1118/1.1569270. [Accessed 8 Jun.
2017].
32. Hsu, S., Cao, Y., Huang,
K., Feng, M. and Balter, J. (2013). Investigation of a method for generating
synthetic CT models from MRI scans of the head and neck for radiation therapy. Physics in Medicine and Biology, [online]
58(23), pp.8419-8435. Available at: http://dx.doi.org/10.1088/0031-9155/58/23/8419. [Accessed
8 Jun. 2017].
33.
Khateri, P., Rad, H., Jafari, A. and Ay, M. (2014). A novel segmentation
approach for implementation of MRAC in head PET/MRI employing Short-TE MRI and
2-point Dixon method in a fuzzy C-means framework. Nuclear Instruments and
Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment,
[online] 734, pp.171-174. Available at: http://dx.doi.org/10.1016/j.nima.2013.09.006. [Accessed 8 Jun. 2017].
34. Khateri, P., Saligheh Rad, H.,
Jafari, A., FathiKazerooni, A., Akbarzadeh, A., ShojaeMoghadam, M., Aryan, A.,
Ghafarian, P. and Ay, M. (2015). Generation of a Four-Class Attenuation Map for
MRI-Based Attenuation Correction of PET Data in the Head Area Using a Novel
Combination of STE/Dixon-MRI and FCM Clustering.
Molecular Imaging and Biology, [online] 17(6), pp.884-892. Available
at: http://dx.doi.org/10.1007/s11307-015-0849-1. [Accessed 8 Jun.
2017].
35. Boettger, T., Nyholm, T.,
Karlsson, M., Nunna, C. and Celi, J. (2008). Radiation therapy planning and
simulation with magnetic resonance images. Medical
imaging, [online] Vol. 6918 (69181C-1). Available
at: http://dx.doi.org/10.1117/12.770016.
36. Rahmer, J., Blume, U. and
Börnert, P. (2007). Selective 3D ultrashort TE imaging: comparison of
"dual-echo" acquisition and magnetization preparation for improving
short-T2 contrast. Magnetic Resonance
Materials in Physics, Biology and Medicine, [online] 20(2),
pp.83-92. Available at: http://dx.doi.org/10.1007/s10334-007-0070-6. [Accessed 8 Jun. 2017].
37. Rank, C., Tremmel, C.,
Hünemohr, N., Nagel, A., Jäkel, O. and Greilich, S. (2013). MRI-based treatment
plan simulation and adaptation for ion radiotherapy using a
classification-based approach. Radiation
Oncology, [online] 8(1), p.51. Available at: http://dx.doi.org/10.1186/1748-717x-8-51. [Accessed
8 Jun. 2017].
38. Navalpakkam, B., Braun, H.,
Kuwert, T. and Quick, H. (2013). Magnetic Resonance Based Attenuation
Correction for PET/MR Hybrid Imaging Using Continuous Valued Attenuation Maps. Investigative Radiology, [online] 48(5),
pp.323-332. Available at: http://dx.doi.org/10.1097/rli.0b013e318283292f. [Accessed 8 Jun.
2017].
39. Liu, L., Jolly, S., Cao,
Y., Vineberg, K., Fessler, J. and Balter, J. (2017). Female pelvic synthetic CT
generation based on joint intensity and shape analysis. Physics in Medicine and Biology, [online]
62(8), pp.2935-2949. Available at: http://dx.doi.org/10.1088/1361-6560/62/8/2935. [Accessed 8 Jun.
2017].
40. Liu, L., Cao, Y., Fessler,
J., Jolly, S. and Balter, J. (2015). A female pelvic bone shape model for
air/bone separation in support of synthetic CT generation for radiation therapy. Physics in Medicine and Biology,
[online] 61(1), pp.169-182. Available at: http://dx.doi.org/10.1088/0031-9155/61/1/169. [Accessed 8 Jun.
2017].
41. Bredfeldt, J., Liu, L.,
Feng, M., Cao, Y. and Balter, J. (2017). Synthetic CT for MRI-based liver stereotactic
body radiotherapy treatment planning. Physics
in Medicine and Biology, [online] 62(8), pp.2922-2934. Available at:
http://dx.doi.org/10.1088/1361-6560/aa5059. [Accessed 8 Jun.
2017].
42. Peng, Z., Zhong, J., Wee,
W. and Lee, J. (2005). Automated vertebra detection and segmentation from the
whole spine MR images. In: IEEE 27th annual
international conference of the engineering in medicine and biology society,
[online] pp.2527-2530, Available at: http://dx.doi.org/10.1109/IEMBS.2005.1616983.
43. Szu-Hao Huang, Yi-Hong Chu,
Shang-Hong Lai and Novak, C. (2009). Learning-Based Vertebra Detection and
Iterative Normalized-Cut Segmentation for Spinal MRI. IEEE Transactions on Medical Imaging,
[online] 28(10), pp.1595-1605. Available at: http://dx.doi.org/10.1109/tmi.2009.2023362. [Accessed 9 Jun.
2017].
44. Andreasen, D., Van Leemput,
K., Hansen, R., Andersen, J. and Edmund, J. (2015). Patch-based generation of a
pseudo CT from conventional MRI sequences for MRI-only radiotherapy of the
brain. Medical Physics, [online]
42(4), pp.1596-1605. Available at: http://dx.doi.org/10.1118/1.4914158. [Accessed
8 Jun. 2017].
45. Edmund, J., Kjer, H., Van
Leemput, K., Hansen, R., Andersen, J. and Andreasen, D. (2014). A voxel-based
investigation for MRI-only radiotherapy of the brain using ultra short echo
times. Physics in Medicine and Biology,
[online] 59(23), pp.7501-7519. Available at: http://dx.doi.org/10.1088/0031-9155/59/23/7501. [Accessed 8 Jun.
2017].
46. Wu, Y., Yang, W., Lu, L.,
Lu, Z., Zhong, L., Huang, M., Feng, Y., Feng, Q. and Chen, W. (2016).
Prediction of CT Substitutes from MR Images Based on Local Diffeomorphic
Mapping for Brain PET Attenuation Correction.
Journal of Nuclear Medicine, [online] 57(10), pp.1635-1641.
Available at: http://dx.doi.org/10.2967/jnumed.115.163121. [Accessed 8 Jun.
2017].
47.
Roy, S., Carras, A., Jog, A., Prince, L. and Lee, J. (2014). MR to CT
registration of brains using image synthesis. In SPIE Medical Imaging, [online] 9034. Available at: http://dx.doi.org/10.1117/12.2043954.
48. Roy, S., Wang, W., Carass,
A., Prince, J., Butman, J. and Pham, D. (2014). PET Attenuation Correction
Using Synthetic CT from Ultrashort Echo-Time MR Imaging. Journal of Nuclear Medicine, [online]
55(12), pp.2071-2077. Available at: http://dx.doi.org/10.2967/jnumed.114.143958. [Accessed 8 Jun.
2017].
49. Johansson, A., Karlsson, M.
and Nyholm, T. (2011). CT substitute derived from MRI sequences with ultrashort
echo time. Medical Physics,
[online] 38(5), pp.2708-2714. Available at: http://dx.doi.org/10.1118/1.3578928. [Accessed 8 Jun.
2017].
50. Johansson, A., Karlsson,
M., Yu, J., Asklund, T. and Nyholm, T. (2012). Voxel-wise uncertainty in CT
substitute derived from MRI. Medical Physics,
[online] 39(6Part1), pp.3283-3290. Available
at: http://dx.doi.org/10.1118/1.4711807. [Accessed
8 Jun. 2017].
51. Johansson, A., Garpebring,
A., Karlsson, M., Asklund, T. and Nyholm, T. (2013). Improved quality of
computed tomography substitute derived from magnetic resonance (MR) data by
incorporation of spatial information--potential application for MR-only
radiotherapy and attenuation correction in positron emission tomography. ActaOncologica, [online] 52(7),
pp.1369-1373. Available at: http://dx.doi.org/10.3109/0284186x.2013.819119. [Accessed 8 Jun.
2017].
52. Kapanen, M. and Tenhunen,
M. (2012). T1/T2*-weighted MRI provides clinically relevant pseudo-CT density
data for the pelvic bones in MRI-only based radiotherapy treatment planning. ActaOncologica, [online] 52(3),
pp.612-618. Available at: http://dx.doi.org/10.3109/0284186x.2012.692883. [Accessed 8 Jun.
2017].
53. Kim, J., Glide-Hurst, C.,
Doemer, A., Wen, N., Movsas, B. and Chetty, I. (2015). Implementation of a
Novel Algorithm For Generating Synthetic CT Images From Magnetic Resonance
Imaging Data Sets for Prostate Cancer Radiation Therapy. International Journal of Radiation
Oncology*Biology*Physics, [online] 91(1), pp.39-47. Available at: http://dx.doi.org/10.1016/j.ijrobp.2014.09.015. [Accessed 8 Jun.
2017].
54. Korhonen, J., Kapanen, M.,
Keyriläinen, J., Seppälä, T. and Tenhunen, M. (2013). A dual model HU
conversion from MRI intensity values within and outside of bone segment for
MRI-based radiotherapy treatment planning of prostate cancer. Medical Physics, [online] 41(1), p.011704.
Available at: http://dx.doi.org/10.1118/1.4842575. [Accessed 8 Jun.
2017].
55. Zhong, L., Lin, L., Lu, Z.,
Wu, Y., Lu, Z., Huang, M., Yang, W. and Feng, Q. (2016). Predict CT image from
MRI data using KNN-regression with learned local descriptors. In: IEEE 13th international symposium on Biomedical
imaging, [online] pp.743-746, Available at: http://dx.doi.org/10.1109/ISBI.2016.7493373.
56. Zhen, X., Wang, Z., Yu, M.
and Li, S. (2015). Supervised descriptor learning for multi-output regression.
In: EEE Conference on computer vision and
pattern recognition, [online] pp.1211-1218, Available at: http://dx.doi.org/10.1109/CVPR.2015.7298725.
57. Huynh, T., Gao, Y., Kang,
J., Wang, L., Zhang, P., Lian, J. and Shen, D. (2016). Estimating CT Image From
MRI Data Using Structured Random Forest and Auto-Context Model. IEEE Transactions on Medical Imaging,
[online] 35(1), pp.174-183. Available at: http://dx.doi.org/10.1109/tmi.2015.2461533. [Accessed
8 Jun. 2017].
58. Brown, L. (1992). A survey
of image registration techniques. ACM
Computing Surveys, [online] 24(4), pp.325-376. Available at: http://dx.doi.org/10.1145/146370.146374. [Accessed 8 Jun. 2017].
59. Rueckert, D and Schnabel.
J. A. (2010) Medical image registration.Biomedical
Image Processing, Springer, [online] pp. 131-154. Available at: http://dx.doi.org/10.1016/10.1007/978-3-642-15816-2_5.
60. Zitová, B. and Flusser, J.
(2003). Image registration methods: a survey. Image
and Vision Computing, [online] 21(11), pp.977-1000. Available at: http://dx.doi.org/10.1016/s0262-8856(03)00137-9. [Accessed 8 Jun.
2017].
61. Maintz, J. and Viergever,
M. (1998). A survey of medical image registration. Medical Image Analysis, [online] 2(1), pp.1-36. Available
at: http://dx.doi.org/10.1016/s1361-8415(01)80026-8. [Accessed 8 Jun.
2017].
62.
Modersitzki, J. (2004). Numerical methods for image registration. Oxford :Oxford
Univ Press on demand.
63.
Hajnal, J., Hill, D.L.G. and Hawkes, D.J (2001). Medical image
registration. CRC Press.
64. Devic, S. (2012). MRI
simulation for radiotherapy treatment planning.
Medical Physics, [online] 39(11), pp.6701-6711. Available at: http://dx.doi.org/10.1118/1.4758068. [Accessed 8 Jun.
2017].
65. Lester, H. and Arridge, S.
(1999). A survey of hierarchical non-linear medical image registration. Pattern Recognition, [online] 32(1),
pp.129-149. Available at: http://dx.doi.org/10.1016/s0031-3203(98)00095-8. [Accessed 8 Jun.
2017].
66. Kops, E. and Hersog, H.
(2007). Alternative methods for attenuation correction for PET images in MR-PET
scanners. In: IEEE Nuclear science symposium
conference record, [online] 6, pp.4327-4330. Available at: http://dx.doi.org/10.1109/NSSMIC.2007.4437073. [Accessed 8 Jun.
2017].
67. Schreibmann, E., Nye, J.,
Schuster, D., Martin, D., Votaw, J. and Fox, T. (2010). MR-based attenuation
correction for hybrid PET-MR brain imaging systems using deformable image
registration. Medical Physics,
[online] 37(5), pp.2101-2109. Available at: http://dx.doi.org/10.1118/1.3377774. [Accessed 8 Jun.
2017].
68. Greer, P., Dowling, J.,
Lambert, J., Frippe, J., Parker, J., Denham, J., Wratten, C., Capp, A. and
Salvado, O. (2011). A magnetic resonance imaging-based workflow for planning
radiation therapy for prostate cancer. Medical journal of Australia,
[online] 194(4), pp.S24-S27. PMID:
21401484.
69.
Dowling, J., Lambert, J., Parker, J., Salvado, O., Fripp, J., Capp, A.,
Wratten, C., Denham, J. and Greer, P. (2012). An Atlas-Based Electron Density
Mapping Method for Magnetic Resonance Imaging (MRI)-Alone Treatment Planning
and Adaptive MRI-Based Prostate Radiation Therapy. International Journal of Radiation Oncology*Biology*Physics,
[online] 83(1), pp.e5-e11. Available at: http://dx.doi.org/10.1016/j.ijrobp.2011.11.056. [Accessed 8 Jun. 2017].
70. Burgos, N., Cardoso, M.,
Thielemans, K., Duncan, J., Atkinson, D., Arridge, S., Hutton, B. and Ourselin,
S. (2014). Attenuation correction synthesis for hybrid PET-MR scanners:
validation for brain study applications. EJNMMI
Physics, [online] 1(1), p.A52. Available at: http://dx.doi.org/10.1186/2197-7364-1-s1-a52. [Accessed 8 Jun.
2017].
71. Uh, J., Merchant, T., Li,
Y., Li, X. and Hua, C. (2014). MRI-based treatment planning with pseudo CT
generated through atlas registration. Medical
Physics, [online] 41(5), p.051711. Available at: http://dx.doi.org/10.1118/1.4873315. [Accessed
8 Jun. 2017].
72. Sjölund, J., Forsberg, D.,
Andersson, M. and Knutsson, H. (2015). Generating patient specific pseudo-CT of
the head from MR using atlas-based regression. Physics
in Medicine and Biology, [online] 60(2), pp.825-839. Available at: http://dx.doi.org/10.1088/0031-9155/60/2/825. [Accessed 8 Jun.
2017].
73. Knutsson, H. and Andersson,
M. (2005). Morphons: segmentation using elastic canvas and paint on priors. In:
IEEE International conference on image
processing, [online] 2, pp.II-1226. Available
at: http://dx.doi.org/10.1009/ICIP.2005.1530283. [Accessed 8 Jun. 2017].
74. Mérida, I., Costes, N.,
Heckemann, R. and Hammers, A. (2015). Pseudo-CT generation in brain MR-PET
attenuation correction: comparison of several multi-atlas methods. EJNMMI Physics, [online] 2(1), p.A29.
Available at: http://dx.doi.org/10.1186/2197-7364-2-s1-a29. [Accessed 8 Jun.
2017].
75. Arabi, H., Koutsouvelis,
N., Rouzaud, M., Miralbell, R. and Zaidi, H. (2016). Atlas-guided generation of
pseudo-CT images for MRI-only and hybrid PET/MRI-guided radiotherapy treatment
planning. Physics in Medicine and Biology,
[online] 61(17), pp.6531-6552. Available at: http://dx.doi.org/10.1088/0031-9155/61/17/6531. [Accessed 8 Jun.
2017].
76. Kraus, K., Jäkel, O.,
Niebuhr, N. and Pfaffenberger, A. (2017). Generation of synthetic CT data using
patient specific daily MR image data and image registration. Physics in Medicine and Biology, [online]
62(4), pp.1358-1377. Available at: http://dx.doi.org/10.1088/1361-6560/aa5200. [Accessed 8 Jun.
2017].
77. Izquierdo-Garcia,
D., Hansen, A., Forster, S., Benoit, D., Schachoff, S., Furst, S., Chen, K.,
Chonde, D. and Catana, C. (2014). An SPM8-Based Approach for Attenuation Correction Combining Segmentation
and Nonrigid Template Formation: Application to Simultaneous PET/MR Brain
Imaging. Journal of Nuclear Medicine,
[online] 55(11), pp.1825-1830. Available at: http://dx.doi.org/10.2967/jnumed.113.136341. [Accessed 8 Jun.
2017].
78. Hofmann, M., Steinke, F.,
Scheel, V., Charpiat, G., Farquhar, J., Aschoff, P., Brady, M., Scholkopf, B.
and Pichler, B. (2008). MRI-Based Attenuation Correction for PET/MRI: A Novel
Approach Combining Pattern Recognition and Atlas Registration. Journal of Nuclear Medicine, [online]
49(11), pp.1875-1883. Available at: http://dx.doi.org/10.2967/jnumed.107.049353. [Accessed 8 Jun.
2017].
79. Chen, Y., Juttukonda, M.,
Lee, Y., Su, Y., Espinoza, F., Lin, W., Shen, D., Lulash, D. and An, H. (2014).
MRI based attenuation correction for PET/MRI via MRF segmentation and sparse
regression estimated CT. In: IEEE 11th
international symposium on Biomedical imaging, [online] 60(2),
pp.1364-1367. Available at: http://dx.doi.org/10.1109/ISBI.2014.6868131. [Accessed 8 Jun. 2017].
80. Siversson, C., Nordström,
F., Nilsson, T., Nyholm, T., Jonsson, J., Gunnlaugsson, A. and Olsson, L.
(2015). Technical Note: MRI only prostate radiotherapy planning using the
statistical decomposition algorithm. Medical
Physics, [online] 42(10), pp.6090-6097. Available at: http://dx.doi.org/10.1118/1.4931417. [Accessed 8 Jun.
2017].
81. Burgos, N., Guerreiro, F.,
McClelland, J., Presles, B., Modat, M., Nill, S., Dearnaley, D., deSouza, N.,
Oelfke, U., Knopf, A., Ourselin, S. and Jorge Cardoso, M. (2017). Iterative
framework for the joint segmentation and CT synthesis of MR images: application
to MRI-only radiotherapy treatment planning.
Physics in Medicine and Biology, [online] 62(11), pp.4237-4253.
Available at: http://dx.doi.org/10.1088/1361-6560/aa66bf. [Accessed 8 Jun.
2017].
82. Demol, B., Boydev, C.,
Korhonen, J. and Reynaert, N. (2016). Dosimetric characterization of MRI-only
treatment planning for brain tumors in atlas-based pseudo-CT images generated
from standard T1-weighted MR images. Medical
Physics, [online] 43(12), pp.6557-6568. Available at: http://dx.doi.org/10.1118/1.4967480. [Accessed 8 Jun.
2017].
83. Wang, Z., Bovik, A.,
Sheikh, H. and Simoncelli, E. (2004). Image Quality Assessment: From Error
Visibility to Structural Similarity. IEEE
Transactions on Image Processing, [online] 13(4), pp.600-612.
Available at: http://dx.doi.org/10.1109/tip.2003.819861. [Accessed 8 Jun.
2017].
84. Stanescu, T., Jans, H.,
Pervez, N., Stavrev, P. and Fallone, B. (2008). A study on the magnetic
resonance imaging (MRI)-based radiation treatment planning of intracranial
lesions. Physics in Medicine and Biology,
[online] 53(13), pp.3579-3593. Available at: http://dx.doi.org/10.1088/0031-9155/53/13/013. [Accessed
8 Jun. 2017].
85. Catana, C., van der Kouwe,
A., Benner, T., Michel, C., Hamm, M., Fenchel, M., Fischl, B., Rosen, B.,
Schmand, M. and Sorensen, A. (2010). Toward Implementing an MRI-Based PET
Attenuation-Correction Method for Neurologic Studies on the MR-PET Brain
Prototype. Journal of Nuclear Medicine,
[online] 51(9), pp.1431-1438. Available at: http://dx.doi.org/10.2967/jnumed.109.069112. [Accessed 8 Jun.
2017].
86. Keereman, V., Fierens, Y.,
Broux, T., De Deene, Y., Lonneux, M. and Vandenberghe, S. (2010). MRI-Based
Attenuation Correction for PET/MRI Using Ultrashort Echo Time Sequences. Journal of Nuclear Medicine, [online]
51(5), pp.812-818. Available at: http://dx.doi.org/10.2967/jnumed.109.065425. [Accessed
8 Jun. 2017].
87. Aitken, A., Giese, D.,
Tsoumpas, C., Schleyer, P., Kozerke, S., Prieto, C. and Schaeffter, T. (2013).
Improved UTE-based attenuation correction for cranial PET-MR using dynamic
magnetic field monitoring. Medical Physics,
[online] 41(1), p.012302. Available at: http://dx.doi.org/10.1118/1.4837315. [Accessed 8 Jun.
2017].
88. Buerger, C., Aitken, A.,
Tsoumpas, C., King, A., Schulz, V., Marsden, P. and Schaeffer, T. (2011).
Investigation of 4D PET attenuation correction using ultra-short-echo time MR.
In: Nuclear science symposium and medical
imaging conference (NSS/MIC). IEEE, [online] 60(2), pp.3558-3561.
Available at: http://dx.doi.org/10.1109/NSSMIC.2011.6153668. [Accessed 8 Jun.
2017].
89. Ghose, S., Dowling, J.,
Rai, R. and Liney, G. (2017). Substitute CT generation from a single ultra
short time echo MRI sequence: preliminary study.
Physics in Medicine and Biology, [online] 62(8), pp.2950-2960.
Available at: http://dx.doi.org/10.1088/1361-6560/aa508a. [Accessed 8 Jun.
2017].
90. Juttukonda, M., Mersereau,
B., Chen, Y., Su, Y., Rubin, B., Benzinger, T., Lalush, D. and An, H. (2015).
MR-based attenuation correction for PET/MRI neurological studies with
continuous-valued attenuation coefficients for bone through a conversion from
R2* to CT-Hounsfield units. NeuroImage,
[online] 112, pp.160-168. Available at: http://dx.doi.org/10.1016/j.neuroimage.2015.03.009. [Accessed 8 Jun. 2017].
91. Delso, G., Wiesinger, F.,
Sacolick, L., Kaushik, S., Shanbhag, D., Hullner, M. and Veit-Haibach, P.
(2015). Clinical Evaluation of Zero-Echo-Time MR Imaging for the Segmentation
of the Skull. Journal of Nuclear Medicine,
[online] 56(3), pp.417-422. Available at: http://dx.doi.org/10.2967/jnumed.114.149997. [Accessed 8 Jun.
2017].
92. Wiesinger, F., Sacolick,
L., Menini, A., Kaushik, S., Ahn, S., Veit-Haibach, P., Delso, G. and Shanbhag,
D. (2015). Zero TEMR bone imaging in the head. Magnetic
Resonance in Medicine, [online] 75(1), pp.107-114. Available at: http://dx.doi.org/10.1002/mrm.25545. [Accessed 8 Jun. 2017].
93. Kim, J., Lee, J., Song, I.
and Lee, D. (2012). Comparison of Segmentation-Based Attenuation Correction
Methods for PET/MRI: Evaluation of Bone and Liver Standardized Uptake Value
with Oncologic PET/CT Data. Journal of
Nuclear Medicine, [online] 53(12), pp.1878-1882. Available at: http://dx.doi.org/10.2967/jnumed.112.104109. [Accessed 8 Jun.
2017].
94. Reza
Ay, M., Akbarzadeh, A., Ahmadian, A. and Zaidi, H. (2014). Classification of bones from MR images in torso PET-MR imaging using a
statistical shape model. Nuclear Instruments
and Methods in Physics Research Section A: Accelerators, Spectrometers,
Detectors and Associated Equipment, [online] 734, pp.196-200.
Available at: http://dx.doi.org/10.1016/j.nima.2013.09.007. [Accessed 8 Jun. 2017].
95.
Aljabar, P., Heckemann, R., Hammers, A., Hajnal, J. and Rueckert, D.
(2009). Multi-atlas based segmentation of brain images: Atlas selection and its
effect on accuracy. NeuroImage,
[online] 46(3), pp.726-738. Available at: http://dx.doi.org/10.1016/j.neuroimage.2009.02.018. [Accessed 8 Jun. 2017].
96. Artaechevarria,
X., Munoz-Barrutia, A. and Ortiz-de-Solorzano, C. (2009). Combination Strategies in Multi-Atlas Image Segmentation: Application to
Brain MR Data. IEEE Transactions on Medical
Imaging, [online] 28(8), pp.1266-1277. Available at: http://dx.doi.org/10.1109/tmi.2009.2014372. [Accessed
8 Jun. 2017].
97.
Mehranian, A., Arabi, H. and Zaidi, H. (2016). Quantitative analysis of
MRI-guided attenuation correction techniques in time-of-flight brain PET/MRI. NeuroImage, [online] 130, pp.123-133.
Available at: http://dx.doi.org/10.1016/j.neuroimage.2016.01.060. [Accessed 8 Jun. 2017].
98. Ren, S., Hara, W., Wang,
L., Buyyounouski, M., Le, Q., Xing, L. and Li, R. (2017). Robust Estimation of
Electron Density From Anatomic Magnetic Resonance Imaging of the Brain Using a
Unifying Multi-Atlas Approach. International
Journal of Radiation Oncology*Biology*Physics, [online] 97(4),
pp.849-857. Available at: http://dx.doi.org/10.1016/j.ijrobp.2016.11.053. [Accessed
8 Jun. 2017].
99. Whelan, B., Kumar, S.,
Dowling, J., Begg, J., Lambert, J., Lim, K., Vinod, S., Greer, P. and Holloway,
L. (2015). Utilising pseudo-CT data for dose calculation and plan optimization
in adaptive radiotherapy. Australasian
Physical & Engineering Sciences in Medicine, [online] 38(4),
pp.561-568. Available at: http://dx.doi.org/10.1007/s13246-015-0376-z. [Accessed 8 Jun.
2017].
100. Zerda, A., Armbruster, B.
and Xing, L. (2007). Formulating adaptive radiation therapy (ART) treatment
planning into a closed-loop control framework. Physics
in Medicine and Biology, [online] 52(14), pp.4137-4153. Available
at: http://dx.doi.org/10.1088/0031-9155/52/14/008. [Accessed 8 Jun.
2017].
101. Roberson, P., McLaughlin,
P., Narayana, V., Troyer, S., Hixson, G. and Kessler, M. (2005). Use and
uncertainties of mutual information for computed tomography/magnetic resonance
(CT/MR) registration post permanent implant of the prostate. Medical Physics, [online] 32(2),
pp.473-482. Available at: http://dx.doi.org/10.1118/1.1851920. [Accessed 8 Jun.
2017].
102. Yang, Y., Schreibmann, E.,
Li, T., Wang, C. and Xing, L. (2007). Evaluation of on-board kV cone beam CT
(CBCT)-based dose calculation. Physics in
Medicine and Biology, [online] 52(3), pp.685-705. Available at: http://dx.doi.org/10.1088/0031-9155/52/3/011. [Accessed 8 Jun.
2017].
103. Korsholm, M., Waring, L.
and Edmund, J. (2014). A criterion for the reliable use of MRI-only
radiotherapy. Radiation Oncology,
[online] 9(1), p.16. Available at: http://dx.doi.org/10.1186/1748-717x-9-16. [Accessed 8 Jun.
2017].
104. Walker, A., Liney, G.,
Metcalfe, P. and Holloway, L. (2014). MRI distortion: considerations for MRI
based radiotherapy treatment planning. Australian
Physical & Engineering Sciences in Medicine, [online] 37(1),
pp.103-113. Available at: http://dx.doi.org/10.1007/s13246-014-0252-2. [Accessed
8 Jun. 2017].